Jusqu’ici nous avons croisé les catégories supérieures surtout à travers le livre de Jacob Lurie dans le hashtag #HigherToposTheory
#HigherToposTheory 12: un nouveau guide de lecture de “Higher topos theory” de Jacob Lurie
mais il existe une autre manière de concevoir la progression vers les n-catégories et les ∞-catégories, comme cet article de Paré et Grandis le précise :
La première manière, plus connue, est appelée « forme globulaire » page 1 de l’article.
La deuxième forme est plus générale et dûe à l’école de Charles Ehresmann (1905-1979) qui est associée aux « Cahiers de topologie et de géométrie différentielle catégoriques » qui est lisible en totalité sur le site Numdam ( c’est Andrée Ehresmann, veuve de Charles, qui gère la collection):
http://www.numdam.org/journals/CTGDC
https://fr.m.wikipedia.org/wiki/Charles_Ehresmann
Ce sont les catégories multiples, qui commencent avec les catégories doubles, puis triples, etc…
https://ncatlab.org/nlab/show/double+category
Une catégorie double est un objet interne à Cat, la catégorie des caégories; voir cet ancien article sur la notion très importante de catégorie interne à une autre:
Une catégorie « ordinaire » est une catégorie interne à la catégorie Set des ensembles.
Un théorème stipule un Interdit analogue à celui de Russell pour l’ensemble de tous les ensembles ; il ne peut exister de catégorie interne à elle même :
Une catégorie triple est définie comme catégorie interne à la catégorie des caégories doubles:
https://ncatlab.org/nlab/show/triple+category
et on monte par le même principe l’échelle des catégories multiples : une catégorie multiple de rang n est interne à la catégorie des catégories multiples de rang n-1 :
https://ncatlab.org/nlab/show/n-fold+category
Une catégorie multiple de rang n est une version stricte d’une n-catégorie :
https://ncatlab.org/nlab/show/n-category
la composition des flèches est strictement associative et unitaire (la composition avec la flèche identité est commutative et laisse invariante n’importe quel morphisme), on a des égalités strictes, et non pas à un isomorphisme près .
Les intercatégories sont des catégories triples particulières :
https://ncatlab.org/nlab/show/intercategory
Une catégorie double a deux sortes de morphismes : horizontal et vertical, voir :
Click to access CTGDC_2004__45_3_193_0.pdf
C’est expliqué page 4 sur 49 paragraphe 1.1 « Basics » qui présente deux compositions, des flèches horizontales et des flèches verticales. Il y a en plus les carrés, qui peuvent être vus comme des 2-morphismes (« double celles »), qui se composent entre eux, le bord d’un carré est composé de deux flèches horizontales et deux flèches verticales , voir Page 4 la figure 1, le carré α est constitué des deux flèches verticales u et v et des deux flèches horizontales f et g et s’écrit :
f
(u v )
g
Dans une intercatégorie, il y a les objets (0-cells ) , trois sorte de morphismes (1-cells) : transversal, horizontal, vertical, trois sortes de 2-morphismes, les carrés et une sorte de 3-morphisme entre les carrés : les cubes
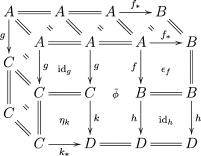
Un bon article sur les intercatégories est celui de Paré et Grandis , d’où sont issues les figures ci dessus :
et bien sûr la page Nlab qui a déjà été donnée:
https://ncatlab.org/nlab/show/intercategory qui donne le lien vers un autre article :
Citons aussi le livre de Grandis « Directed algebraic topology «
Click to access Bk.XXDATXX.pdf
https://ncatlab.org/nlab/show/Directed+Algebraic+Topology
Dans une multicatégorie un morphisme relis un seul objet à une collection de plusieurs objets :
https://ncatlab.org/nlab/show/multicategory
Dans une polycatégories, une liste finie de plusieurs objets peut être reliée à une autre collection de plusieurs objets :
there is nothing to fear but fear itself
Autrement qu'être Mathesis uni∜ersalis Problema Universale Heidegger/Husserl être/conscience : plan vital-ontologique vs plan spirituel d'immanence CLAVIS UNIVERSALIS HENOSOPHIA PANSOPHIA ενοσοφια μαθεσις 
You must be logged in to post a comment.